[알고리즘] 다양한 정렬 (버블, 카운팅, 선택 정렬) - 파이썬
2021. 8. 22. 13:22
반응형
🔹 요약
| 알고리즘 | 평균 수행시간 | 최악 수행시간 | 특징 |
| 버블 정렬 | O(N^2) | O(N^2) | 이해가 쉽다. (코딩이 쉽다) |
| 카운팅 정렬 | O(N+K) | O(N+K) | 비교적 빠르다. |
| 선택 정렬 | O(N^2) | O(N^2) | 수행 회수가 버블&삽입 정렬보다 작다. |
🔹 버블 정렬 (Bubble Sort)
- 인접한 두 개의 원소를 비교하며 자리를 계속 교환하는 방식
- 정렬 과정
- 모든 원소를 이동하며 인접한 원소끼리 크기를 비교하여 자리를 교환한다.
- 한번 전체를 이동하면 가장 큰 원소가 마지막에 위치한다.
- 다시 처음부터 마지막 전까지 정렬한다.
- 시간 복잡도: O(N^2)
파이썬 코드
def bubble_sort(arr):
for end_idx in range(len(arr)-1, 0, -1): # 마지막 지점이다.
for move_idx in range(end_idx): # 비교&교환하며 마지막 이전까지 이동한다.
if arr[move_idx] > arr[move_idx+1]: # 다음값과 비교해서 크면
arr[move_idx], arr[move_idx+1] = arr[move_idx+1], arr[move_idx] # 교환
return arr
sample_list = [5, 4, 8, 6, 1]
sorted_list = bubble_sort(sample_list)
print(sorted_list) # [1, 4, 5, 6, 8]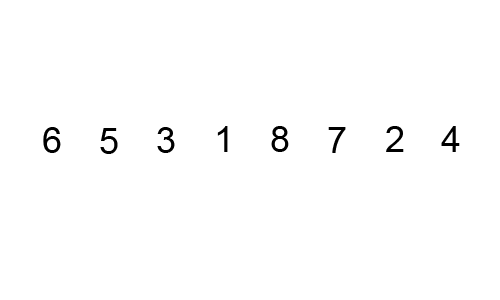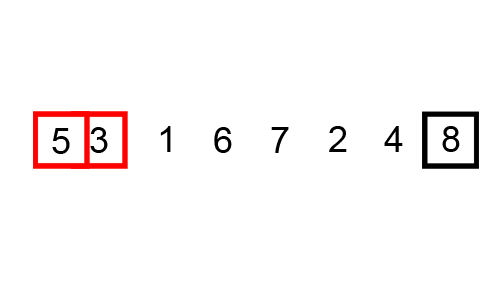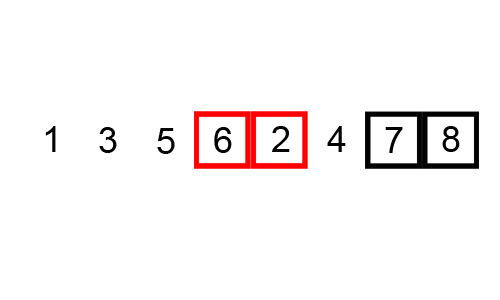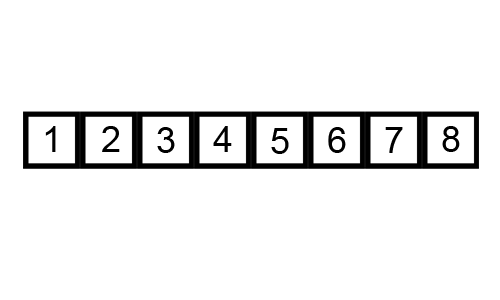
🔹 카운팅 정렬 (Counting Sort)
- 정렬할 리스트에 요소가 몇 개씩 있는지 세는 작업을 하고, 그 결과를 이용해 정렬시킴
- 제한 사항
- 정수를 인덱스로 사용하기 때문에 실수형 요소를 가진 리스트에서는 부적합 함
- 리스트 내의 가장 큰 정수를 알아야 함
- 정렬 과정 (문자만으로 이해가 어렵습니다. 아래 '이해를위한사이트'와 함께 읽어주세요.)
- 총 3개의 리스트를 다룬다. (정렬해야할 리스트, 요소 수를 저장하는 리스트, 정렬된 리스트)
- 정렬해야할 리스트에서 각 요소의 수를 세어 요소 수를 저장하는 리스트에 대입한다.
- 요소 수를 저장하는 리스트에 idx=0부터 끝까지 값을 누적합하며 더해준다.
- 정렬해야할 리스트 끝에서부터 처음으로 내려가면서 요소 수를 저장하는 리스트를 이용하여 정렬된 리스트를 만든다.
- 시간 복잡도: O(N+K), N은 리스트 길이, K는 요소의 최대값
파이썬 코드
def counting_sort(arr):
k = max(arr) # 가장 큰 값
result_list = [0]*len(arr) # 정렬된 리스트
counting_list = [0]*(k+1) # 요소 수를 저장하는 리스트
# counting list 생성
for i in range(len(arr)):
counting_list[arr[i]] += 1 # 정렬할 요소를 idx로 사용
# counting list 누적합
for j in range(1, len(counting_list)):
counting_list[j] += counting_list[j-1] # 누적합하며 더한다.
# result list 원소 넣기
for m in range(len(result_list)-1, -1, -1):
result_list[counting_list[arr[m]]-1] = arr[m]
counting_list[arr[m]] -= 1
return result_list
sample_list = [1, 5, 1, 4, 6, 2, 4]
sorted_list = counting_sort(sample_list)
print(sorted_list) # [1, 1, 2, 4, 4, 5, 6]이해를 위한 사이트 (https://www.cs.usfca.edu/~galles/visualization/CountingSort.html)

🔹 선택 정렬 (Selection Sort)
- 리스트 전체를 확인하여 가장 작은 값을 앞에다가 하나씩 두는 방식
- 정렬 과정
- 리스트에 최소값을 찾는다.
- 리스트 첫번째 값 (idx=0)과 최소값을 교환한다.
- 교환한 값 뒤(idx=1)부터 리스트의 최소값을 찾아 구간 첫번째 값과 교환한다.
- 시간 복잡도: O(N^2)
파이썬 코드
def selection_sort(arr):
for start_idx in range(len(arr)-1): # 구간 시작지점
min_idx = start_idx # 구간 최소값의 idx를 저장하기 위한 초기화
for move_idx in range(start_idx+1, len(arr)): # 구간 순환
if arr[min_idx] > arr[move_idx]: # 최소값 발견하면
min_idx = move_idx # idx 리뉴얼
arr[start_idx], arr[min_idx] = arr[min_idx], arr[start_idx] # 교환
return arr
sample_list = [1, 5, 6, 5, 1, 2, 3]
sorted_list = selection_sort(sample_list)
print(sorted_list) # [1, 1, 2, 3, 5, 5, 6]

반응형
'Programming > 알고리즘' 카테고리의 다른 글
| [C++] 함수 객체 functor (Function Object) (0) | 2023.04.24 |
|---|---|
| [C++] Template 이용하기 (Generic 프로그래밍) (0) | 2023.04.24 |
| [C++] class와 struct 차이. 무엇을 언제 써야할까? (0) | 2023.04.24 |
| [알고리즘] 부분 수열 (w/ 비트 마스크) - 파이썬 (0) | 2021.08.22 |
| [알고리즘] 시간복잡도 & 공간복잡도 (0) | 2021.08.20 |










